An Analysis of Median Income in the ACS 2023

Author

Aparneesh Patil

Question to Ask: Amongst Age, Education, and Race, what is the most significant factor influencing higher median salaries across counties in Missouri? (does a correlation exist?)

First, let’s futher define the factors

Age
- Median Age
Education
- Bachelors Degree or Above (%)
Race
- White only (%)

Side Note: I picked Missouri because that’s where I’m from and chose to use estimates (ACS) because it’s more reliable for small geographies.

Age

Let’s start by examining age. Using the ACS, we identify Table B01002 as the source for median age data. To analyze this alongside income, we extract two separate tables: one for median age and another for median income. We then create two distinct variables, median_age and median_income, corresponding to each dataset.

median_income <- read.csv("data/median_income_acs_23.csv")
median_age <- read.csv("data/median_age_acs_23.csv")

median_income <- select(median_income,-c(X, variable))
median_age <- select(median_age,-c(X, variable))

Since these are two separate datasets, we need to combine them before analysis. Using dplyr’s full_join(), we can merge the datasets based on their shared columns: GEOID and NAME.

combined_tables = full_join(median_age, median_income, by = c("GEOID", "NAME"))
head(combined_tables)

  GEOID                    NAME estimate.x moe.x estimate.y moe.y
1 29001  Adair County, Missouri       29.8   0.7      56583  5235
2 29001  Adair County, Missouri       29.8   0.7      56583  5235
3 29001  Adair County, Missouri       30.0   1.3      56583  5235
4 29003 Andrew County, Missouri       42.1   0.7      74007  5338
5 29003 Andrew County, Missouri       40.8   1.2      74007  5338
6 29003 Andrew County, Missouri       44.1   0.9      74007  5338

The only two columns we need to focus on are estimate.x and estimate.y, which represent median age and median income, respectively. Using these two variables, we can create a plot to explore whether a correlation exists between median age and median income across counties in Missouri.

model = lm(estimate.y ~ estimate.x, data = combined_tables)
print(model)


Call:
lm(formula = estimate.y ~ estimate.x, data = combined_tables)

Coefficients:
(Intercept)   estimate.x  
    91515.3       -771.5

r2 = summary(model)$r.squared

ggplot(combined_tables, aes(x = estimate.x, y = estimate.y)) + 
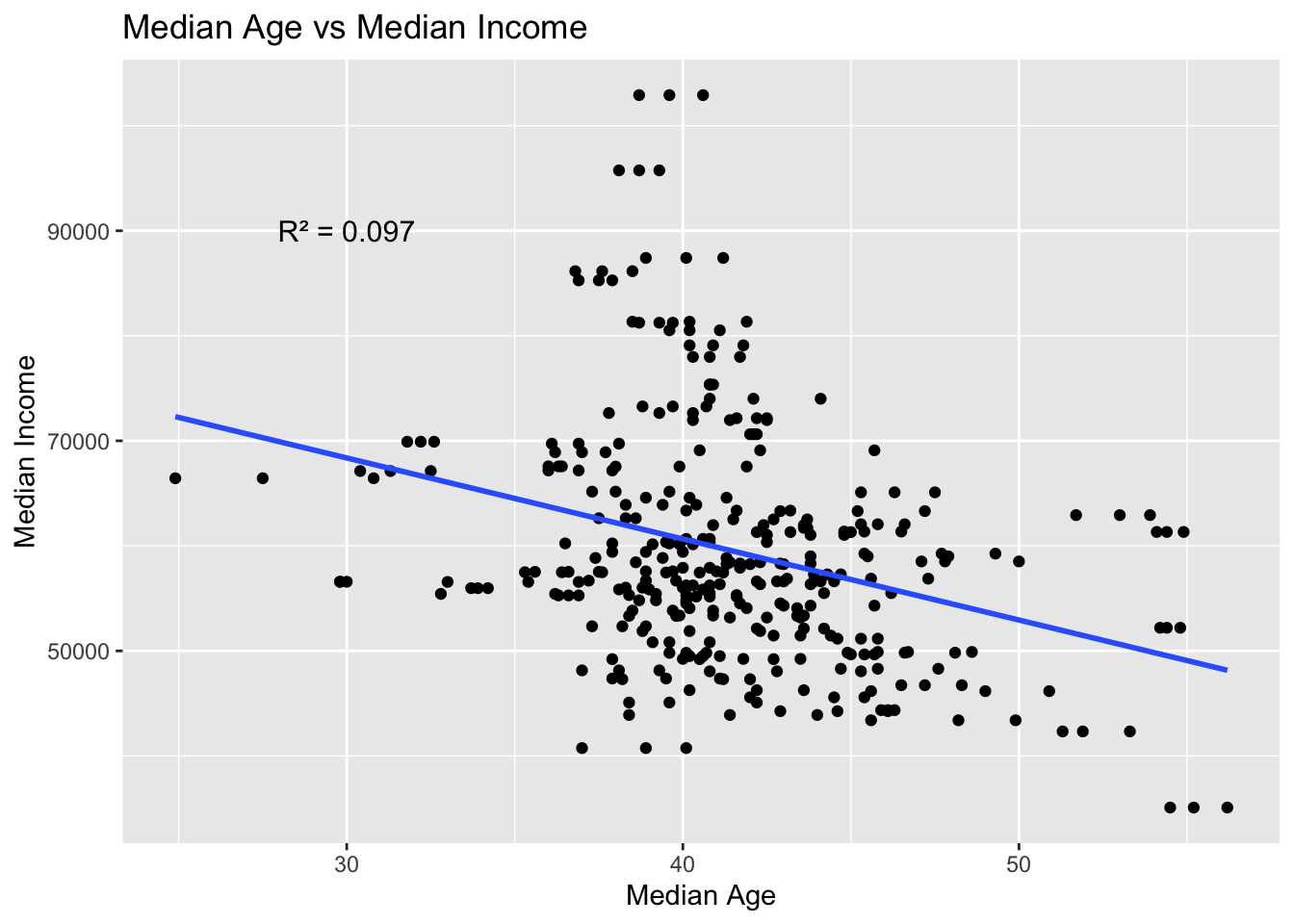
geom_point() + labs(x = "Median Age", y = "Median Income",title = "Median Age vs Median Income") + geom_smooth(method = "lm", se = FALSE) + annotate("text", x = 30, y = 90000, label = paste0("R² = ", round(r2, 3)), size = 4)

`geom_smooth()` using formula = 'y ~ x'

From the scatterplot and also the \(R^2\) value, we observe that there appears to be no correlation between median age and median income. Several factors could explain this. For instance, counties with a higher median age may have a larger retired population, which would naturally lower the median income.

Education

Let’s now move on to the next factor: education, specifically, the percentage of people with a Bachelor’s Degree or higher. Browsing the ACS, we identify Table B15003 as the appropriate source for measuring educational attainment among individuals aged 25 and over. To calculate the percentage of the population with a bachelor’s degree or higher, we sum the values from variables B15003_022E to B15003_025E, and divide this total by B15003_001E, which represents the total population aged 25 and above in the county. We then add this computed percentage as a new column in our dataset and remove all unnecessary columns to retain only the relevant information.

edu_data <- read.csv("data/edu_data_acs_23.csv")

edu_data = mutate(edu_data, percent_bachelors_or_higher = 100 * ( B15003_022E + B15003_023E + B15003_024E + B15003_025E ) / B15003_001E)
edu_simple = transmute(edu_data, GEOID, NAME, percent_bachelors_or_higher)

  GEOID                      NAME percent_bachelors_or_higher
1 29001    Adair County, Missouri                    35.04846
2 29003   Andrew County, Missouri                    26.92247
3 29005 Atchison County, Missouri                    22.04498
4 29007  Audrain County, Missouri                    16.12020
5 29009    Barry County, Missouri                    13.38080
6 29011   Barton County, Missouri                    17.95604

Next, we combine the educational attainment data with the median income data. Using dplyr’s full_join() function, we merge the two datasets based on their shared columns: GEOID and NAME.

combine_age_education = full_join(median_income, edu_simple, by = c("GEOID", "NAME"))
head(combine_age_education)

  GEOID                      NAME estimate  moe percent_bachelors_or_higher
1 29001    Adair County, Missouri    56583 5235                    35.04846
2 29003   Andrew County, Missouri    74007 5338                    26.92247
3 29005 Atchison County, Missouri    59260 5314                    22.04498
4 29007  Audrain County, Missouri    56232 4379                    16.12020
5 29009    Barry County, Missouri    56611 4204                    13.38080
6 29011   Barton County, Missouri    49503 5066                    17.95604

The only two columns we need to focus on are percent_bachelors_or_higher and estimate, which represent percent of bachelors or higher and median income, respectively. Using these two variables, we can create a plot to explore whether a correlation exists between education and median income across counties in Missouri.

model = lm(estimate ~ percent_bachelors_or_higher, data = combine_age_education)
r2 = summary(model)$r.squared
print(model)


Call:
lm(formula = estimate ~ percent_bachelors_or_higher, data = combine_age_education)

Coefficients:
                (Intercept)  percent_bachelors_or_higher  
                      39863                          958

ggplot(combine_age_education, aes(x = percent_bachelors_or_higher, y = estimate)) + 
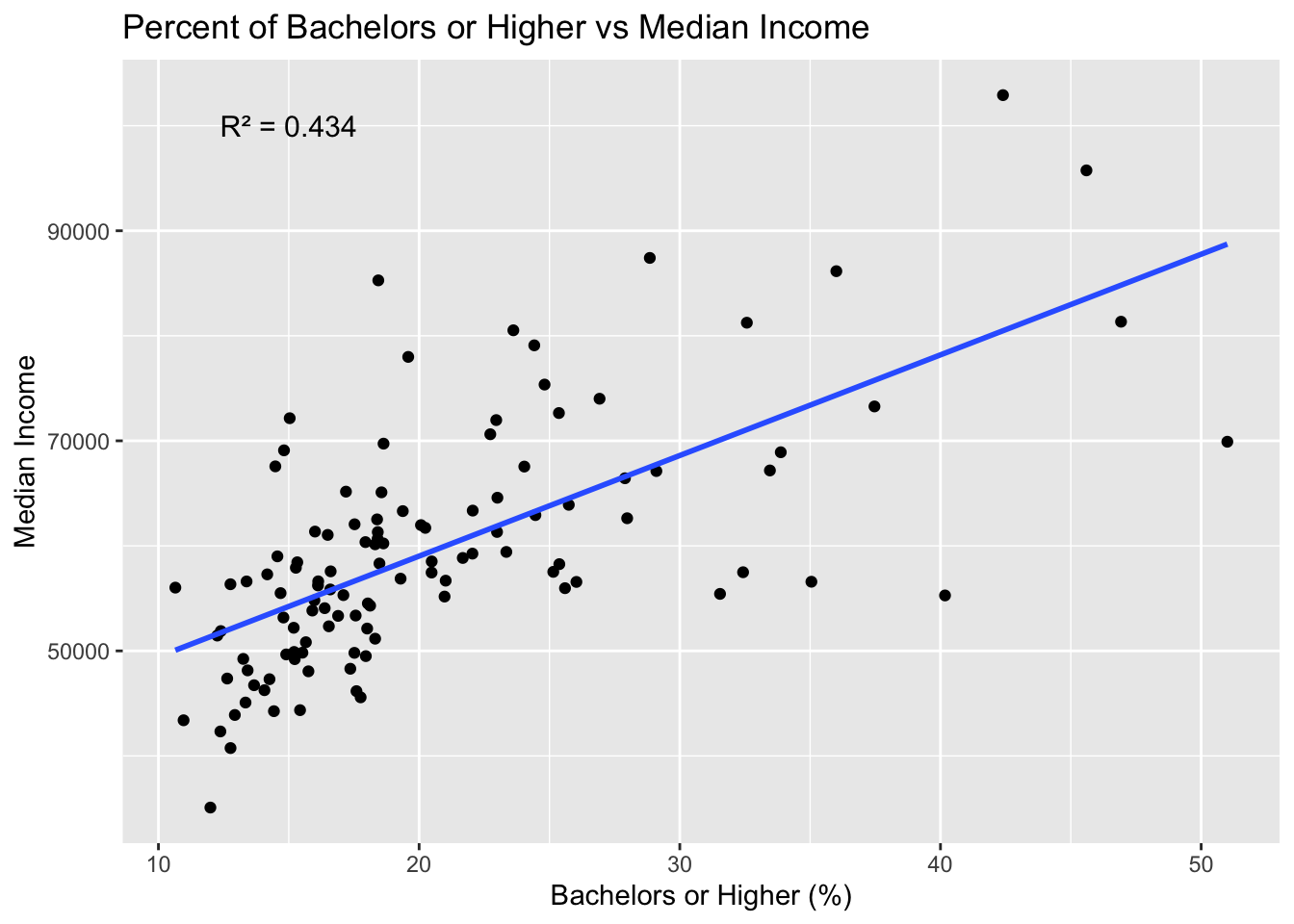
geom_point() + labs(x = "Bachelors or Higher (%)", y = "Median Income",title = "Percent of Bachelors or Higher vs Median Income") + geom_smooth(method = "lm", se = FALSE) + annotate("text", x = 15, y = 100000, label = paste0("R² = ", round(r2, 3)), size = 4)

`geom_smooth()` using formula = 'y ~ x'

From the scatterplot, we observe a moderate correlation between educational attainment and median income. With an \(R^2\) value of 0.43, the relationship is not strong enough to be conclusive, but it does suggest a meaningful association. While other factors may also influence income levels, education appears to be a significant predictor of higher median salaries.

Race

Next, let’s look at race. The ACS provides the Table BO2001 for the race of each location. Using this we can repeat what we did in previous steps to come up with the following:

race_data <- read.csv("data/race_data_acs_23.csv")

race_data = mutate(race_data, percent_white = 100 * (B02001_002E) / B02001_001E)
race_simple = transmute(race_data, GEOID, NAME, percent_white)

  GEOID                      NAME percent_white
1 29001    Adair County, Missouri      88.89946
2 29003   Andrew County, Missouri      93.75207
3 29005 Atchison County, Missouri      94.30598
4 29007  Audrain County, Missouri      89.12022
5 29009    Barry County, Missouri      81.90979
6 29011   Barton County, Missouri      92.07531

Next, we combine the race data with the median income data. Using dplyr’s full_join() function, we merge the two datasets based on their shared columns: GEOID and NAME.

combine_race_income = full_join(median_income, race_simple, by = c("GEOID", "NAME"))
head(combine_race_income)

  GEOID                      NAME estimate  moe percent_white
1 29001    Adair County, Missouri    56583 5235      88.89946
2 29003   Andrew County, Missouri    74007 5338      93.75207
3 29005 Atchison County, Missouri    59260 5314      94.30598
4 29007  Audrain County, Missouri    56232 4379      89.12022
5 29009    Barry County, Missouri    56611 4204      81.90979
6 29011   Barton County, Missouri    49503 5066      92.07531

The only two columns we need to focus on are percent_white and estimate, which represent percent of white people and median income, respectively. Using these two variables, we can create a plot to explore whether a correlation exists between race and median income across counties in Missouri.

model = lm(estimate ~ percent_white, data = combine_race_income)
r2 = summary(model)$r.squared
print(model)


Call:
lm(formula = estimate ~ percent_white, data = combine_race_income)

Coefficients:
  (Intercept)  percent_white  
      77712.1         -203.7

ggplot(combine_race_income, aes(x = percent_white, y = estimate)) + 
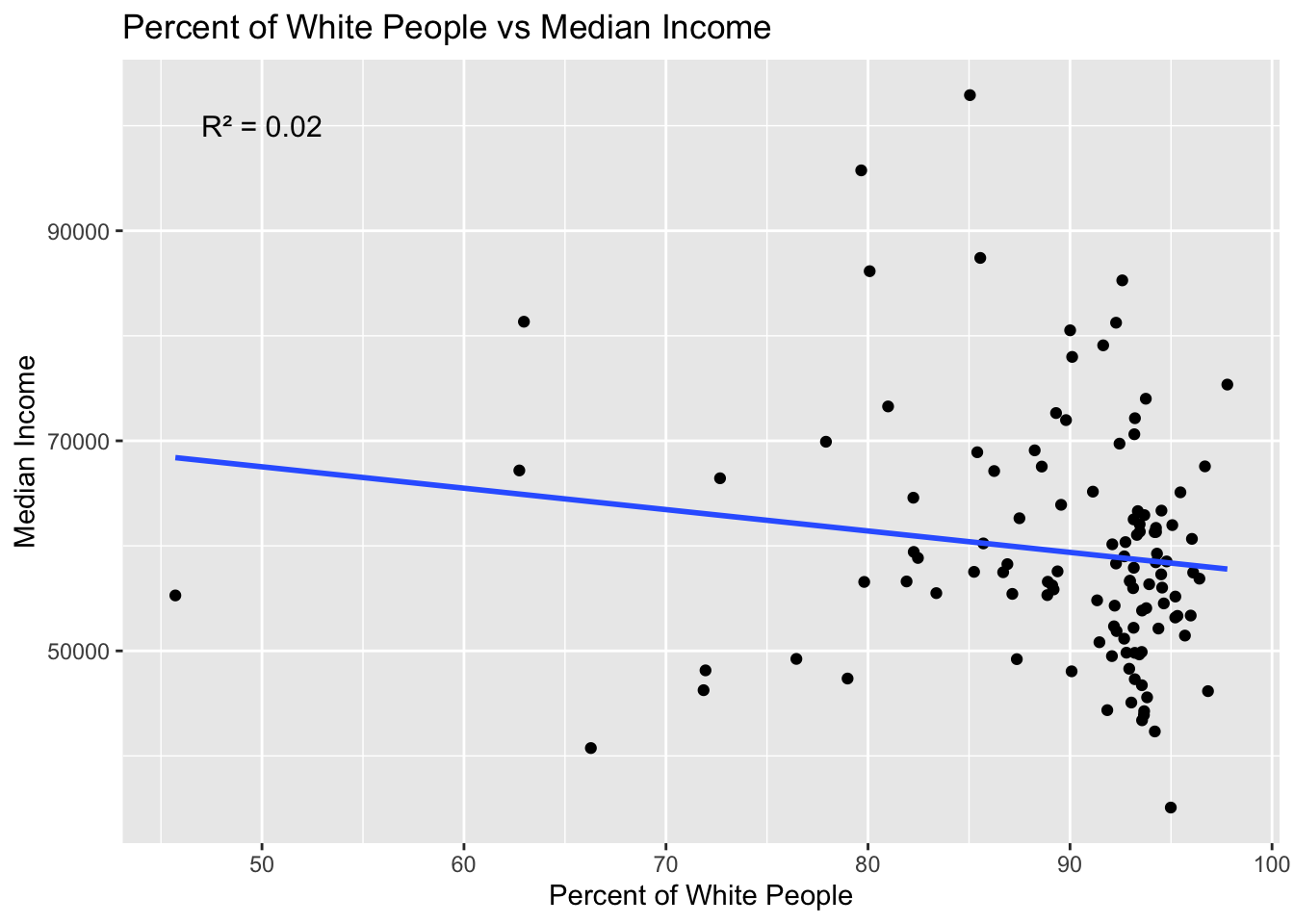
geom_point() + labs(x = "Percent of White People", y = "Median Income",title = "Percent of White People vs Median Income") + annotate("text", x = 50, y = 100000, label = paste0("R² = ", round(r2, 3)), size = 4) + geom_smooth(method = "lm", se = FALSE)

`geom_smooth()` using formula = 'y ~ x'

From the scatterplot and also the \(R^2\) value, we observe that there appears to be no correlation between race and median income.

Conclusion

Among the three factors we examined, education appears to be the most significant predictor of higher median income. In other words, counties in Missouri tend to have higher median salaries as the percentage of residents with a college degree or higher increases.

Limitations

Correlation doesn’t imply Causation
Simplification of Race
Estimates (Margin of Error)
Spatial Limitation (only limited to Missouri)
Multi-factor problem